5º Educación Primaria.
Tema 1: Números naturales.
Este primer tema del curso es un poco de repaso de cursos pasados. "Simplemente", vamos a sumar, restar, multiplicar y dividir. Operaciones que todos deberíais de tener ya más que controladas. Si no es así (sobre todo por culpa de las tablas de multiplicar y la división), pasaros por las secciones propias de 'tablas de multiplicar' y de '¿cómo se dividía?' y las repasáis un poquillo. Sí que os dejo alguna explicación de los últimos puntos del tema: la jerarquía de las operaciones y las potencias.
Jerarquía de las operaciones
Esta jerarquía se tiene en cuenta cuando tenemos que resolver operaciones combinadas. Es decir, cuando tenemos expresiones numéricas con más de una operación diferente. Para ello debemos tener en cuenta esta jerarquía para resolverlas de forma correcta, como podéis ver en las siguientes imágenes.
Potencias. Cuadrados y cubos y potencias de base 10.
En estos últimos puntos del tema, descubrimos las potencias. Que, básicamente, son una multiplicación de factores que se repiten.
Por otro lado, tenemos las potencias de base 10. Se llama así, a la potencia que tiene como base el número 10 y cuyo exponente nos indica el número de ceros de los que irá acompañada la unidad (1) en el resultado.
 |
| Potencias. Cuadrados y cubos. |
 |
| Potencias de base 10. |
Ahora, practica aquí >>
Tema 2: Múltiplos y divisores.
Este segundo tema del curso, tampoco debería resultarnos de gran complejidad. Sigue siendo un tema "de repaso" por lo que los conceptos que trabajaremos son ya conocidos por los chicos. Estos conceptos son los siguientes, que podemos ver resumidos en la imagen.
Ahora, practica aquí (*) >>
La divisibilidad de los números
Divisores de un número
Múltiplos 1
Múltiplos 2
Criterios de divisibilidad
Criterios de divisibilidad 2
Números primos hasta el 100
Números primos y compuestos
(*) En las actividades puede haber algunas cosas que nosotros no hayamos visto en clase; pero nunca está mal ampliar contenidos y conocimientos.
Tema 3: Las fracciones.
A pesar de que el tema de las fracciones siempre tiende a atragantarse, en este curso simplemente hacemos una "aproximación" a las fracciones. Algo bastante sencillito y que viene también bastante bien explicado en el libro. Por lo que creo que no es necesario que ponga ninguna explicación teórica por aquí. Sí que os voy a dejar algunas actividades para que practiquéis.
Practica aquí (*) >>
Comparar fracciones con la unidad 1
Comparar fracciones con la unidad 2
Comparar fracciones 1
Fracción irreducible
Fracciones equivalentes
Fracción de una cantidad (o de un número)
(*) En las actividades puede haber algunas cosas que nosotros no hayamos visto en clase; pero nunca está mal ampliar contenidos y conocimientos.
Tema 4: Operar con fracciones.
Sumar y restar fracciones
Aquí os dejo un par de vídeos donde os recuerda cómo hacerlo y así lo podéis ver tantas veces como queráis. Solo os pongo la suma y resta de fracciones con distinto denominador porque las de igual denominador ya sabéis que son súper fáciles. Simplemente, dejamos el denominador tal y como está y sumamos o restamos los numeradores.
Convertir un número mixto a fracción y viceversa
De igual forma, aquí os dejo un vídeo sobre cómo pasar una fracción a número mixto y al revés. Tened en cuenta que cuando en el vídeo habla de "residuo" se refiere a lo que nosotros llamamos "resto" en una división.
Porcentaje de una cantidad
Finalmente, os dejo otro vídeo para ver cómo se calcula el porcentaje de una cantidad. Esto se hace igual que cuando calculábamos la fracción de un número en el tema anterior. Porque un porcentaje no es más que una fracción con denominador 100.
Practica aquí (*) >>
(*) En las actividades puede haber algunas cosas que nosotros no hayamos visto en clase; pero nunca está mal ampliar contenidos y conocimientos.
Tema 5: Números Decimales.
En este primer tema del 2º trimestre, empezamos a trabajar con los decimales. En este tema vamos a familiarizarnos con ellos para, en el siguiente, hacer operaciones con este tipo de números. Así, lo primero que tenemos que saber de los números decimales son sus partes y cómo se leen >>
Comparar números decimales
Redondear números decimales
Practica aquí (*) >>
(*) En las actividades puede haber algunas cosas que nosotros no hayamos visto en clase; pero nunca está mal ampliar contenidos y conocimientos.
Tema 6: Operar con números decimales.
Una vez que ya nos hemos familiarizado con los números decimales en el tema anterior, ahora vamos a comenzar a operar con ellos. Es decir, vamos a sumar, restar, multiplicar y dividir decimales. Para ello, es muy importante que sepa sumar, restar, multiplicar y dividir PERFECTAMENTE números "normales" (naturales). Si aún tengo dudas con esto, tengo que ponerme a tope las pilas en casa.Sumar y restar números decimales
Multiplicar con números decimales
División con cociente decimal
Dividir con números decimales
Practica aquí (*) >>
(*) En las actividades puede haber algunas cosas que nosotros no hayamos visto en clase; pero nunca está mal ampliar contenidos y conocimientos.
Tema 7: Medir longitudes, capacidades y masas.
Expresar cantidades de forma compleja e incompleja
Os dejo este pequeño video explicativo con dos formas diferentes por las que expresar una cantidad en forma compleja o incompleja.
Os pido disculpas por las faltas de ortografía que aparecen en el texto del vídeo, las tildes, pero la herramienta de texto de la pizarra digital no me dejaba ponerlas.
¡Espero que os ayude al último repasillo!
Os pido disculpas por las faltas de ortografía que aparecen en el texto del vídeo, las tildes, pero la herramienta de texto de la pizarra digital no me dejaba ponerlas.
¡Espero que os ayude al último repasillo!
Pasar de unas unidades a otras
Durante este tema, estamos aprendiendo a operar con unidades de medida. Principalmente, a pasar de unas unidades a otras. Por ejemplo, pasar de metros (m) a decímetros (dm); o pasar de centigramos (cg) a hectogramos (hg). Para ello, es muy importante que nuestr@s chic@s siempre tengan en la cabeza esta escalera que hemos visto en clase y que deberían tener copiada en su libreta. El funcionamiento es muy sencillo: cuando subimos la escalera, es decir, cuando vamos de una unidad más pequeña a otra más grande, dividimos; y cuando bajamos la escalera, es decir, pasamos de una unidad más grande a otra más pequeña, multiplicamos. Teniendo en cuenta que cada unidad es 10 veces más grande que la que está en el escalón inferior y 10 más pequeña que la que tiene en el escalón superior. Así, multiplicaremos o dividiremos por 10, 100, 1000,... dependiendo del número de escalones que bajemos o subamos.
¡A practicar con la escalera!
*
* Esta escalera representa las unidades de longitud; pero con las unidades de masa o capacidad sería exactamente igual. Simplemente, cambiamos las unidades correspondientes.
Practica aquí (*) >>
(*) En las actividades puede haber algunas cosas que nosotros no hayamos visto en clase; pero nunca está mal ampliar contenidos y conocimientos.
Durante este tema, estamos aprendiendo a operar con unidades de medida. Principalmente, a pasar de unas unidades a otras. Por ejemplo, pasar de metros (m) a decímetros (dm); o pasar de centigramos (cg) a hectogramos (hg). Para ello, es muy importante que nuestr@s chic@s siempre tengan en la cabeza esta escalera que hemos visto en clase y que deberían tener copiada en su libreta. El funcionamiento es muy sencillo: cuando subimos la escalera, es decir, cuando vamos de una unidad más pequeña a otra más grande, dividimos; y cuando bajamos la escalera, es decir, pasamos de una unidad más grande a otra más pequeña, multiplicamos. Teniendo en cuenta que cada unidad es 10 veces más grande que la que está en el escalón inferior y 10 más pequeña que la que tiene en el escalón superior. Así, multiplicaremos o dividiremos por 10, 100, 1000,... dependiendo del número de escalones que bajemos o subamos.
*Tema 8: Medir el tiempo y el dinero.
Medida del tiempo
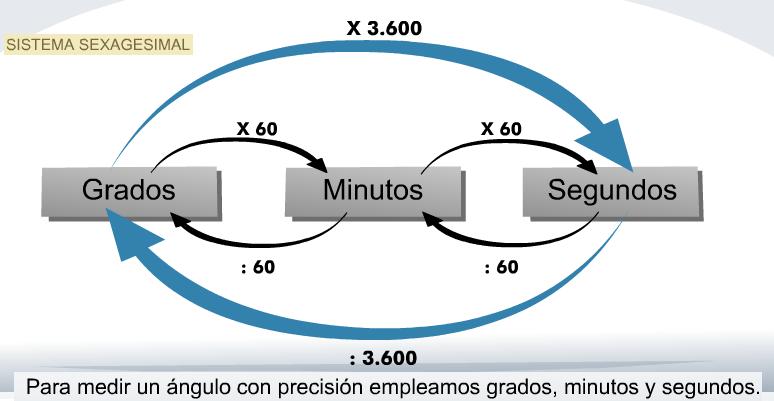
En este nuevo tema seguimos trabajando con la medida de distintas magnitudes. En este caso, trataremos dos muy importante, por muy utilizadas en la vida diaria, como son el tiempo y el dinero. Para medirlas, y pasar de unas unidades a otras, es importante que tengamos en cuenta que el tiempo, en cuanto a horas, minutos y segundos, se fracciona en 60 unidades (sistema sexagesimal), y no en 100 como estamos acostumbrados con las demás magnitudes (sistema decimal). Es decir, que, por ejemplo, una hora NO son 100 minutos, sino 60. Por lo que para pasar de una unidad a otra (entre horas, minutos y segundos), debemos de multiplicar o dividir por 60 y no por 10 como hacíamos con las otras magnitudes.
Distintos modos de expresar medidas de tiempo
Distintos modos de expresar medidas de tiempo
(*) En las actividades puede haber algunas cosas que nosotros no hayamos visto en clase; pero nunca está mal ampliar contenidos y conocimientos.
Tema 9: Ángulos.
En este primer tema del tercer trimestre, vamos a trabajar con los ángulos. Estamos viendo qué es un ángulo, sus partes y los tipos que hay. Todo ello, resumido en las siguientes dos imágenes:
En este primer tema del tercer trimestre, vamos a trabajar con los ángulos. Estamos viendo qué es un ángulo, sus partes y los tipos que hay. Todo ello, resumido en las siguientes dos imágenes:
Además de esto, también estamos trabajando cómo medir y dibujar ángulos; así como, cómo operar (sumar y restar) con sus medidas. Para ello es importante que sepamos manejar el transportador de ángulos y que tengamos en cuenta que la medida de ángulos también "funciona" con el sistema sexagesimal que ya aprendimos en el tema anterior con la medida del tiempo.
Posteriormente, abordaremos cómo trazar la mediatriz de un segmento y la bisectriz de un ángulo. Aquí dejo un par de videos donde nos recuerda muy bien cómo hacerlo.
¡ES MUY IMPORTANTE QUE TODOS TENGAMOS TRANSPORTADOR DE ÁNGULOS, COMPÁS Y REGLA!
Practica aquí (*) >>
(*) En las actividades puede haber algunas cosas que nosotros no hayamos visto en clase; pero nunca está mal ampliar contenidos y conocimientos.
Tema 10: Figuras planas.
Los polígonos (en general).
 |
| Imagen 1. |
En este nuevo tema, seguimos con la geometría, trabajando ahora con los polígonos. Primeramente, aprendemos que un polígono es una línea poligonal cerrada y las partes que tiene (imagen 1). Diferenciando entre polígonos regulares, que tienen todos sus lados y ángulos iguales, e irregulares, que no los tienen todos iguales.
Luego hemos visto la clasificación básica de los polígonos, que depende del número de lados que tienen (imagen 2).
 |
| Imagen 2. |
Finalmente, en esta primera parte, aprendemos que el perímetro de un polígono es la suma de todos sus lados; y que un polígono es convexo si todos sus ángulos interiores son menores de 180º, y cóncavo si tiene algún ángulo mayor de 180º.
Ejercicio tipos de polígono
Ejercicio polígonos cóncavos y convexos
Ejercicio sobre perímetros 1
Ejercicio sobre perímetros 2
Triángulos y cuadriláteros.
Son los dos tipos de polígonos más conocidos por nuestros alumnos.
Como características principales de ambos, podemos destacar:
Triángulos:
- Tienen tres lados.
- Sus ángulos interiores suman 180º.
- En un triángulo rectángulo, los lados que forman el ángulo recto reciben el nombre de catetos y, el otro lado, el de hipotenusa.
Cuadriláteros:
- Tienen cuatro lados.
- Sus ángulos interiores suman 360º.
- La diagonal es un segmento que une dos vértices no consecutivos.
Son los dos tipos de polígonos más conocidos por nuestros alumnos. 
- Sus ángulos interiores suman 180º.- En un triángulo rectángulo, los lados que forman el ángulo recto reciben el nombre de catetos y, el otro lado, el de hipotenusa.
La circunferencia y el círculo.
Para diferenciar estos dos elementos relacionados, podemos decir que la circunferencia es el contorno y el círculo el interior. Por ejemplo: una circunferencia sería un aro, y un círculo una pizza o una moneda.
En este apartado nos acercaremos a las fórmulas matemáticas para calcular la longitud de una circunferencia.
L (longitud de la circunferencia) = D (diámetro) x "número pi" = 2 x "número pi" x r (radio).
Explicación de la fórmula para calcular la longitud de una circunferencia
Ejercicio sobre elementos de la circunferencia y rectas
Ejercicio sobre las partes de una circunferencia
Pasapalabra sobre geometría (Algunas preguntas no las hemos visto aún, pero las iremos viendo en lo que queda de curso. Puede ser un buen ejercicio de ampliación de conocimientos).
Para diferenciar estos dos elementos relacionados, podemos decir que la circunferencia es el contorno y el círculo el interior. Por ejemplo: una circunferencia sería un aro, y un círculo una pizza o una moneda.
En este apartado nos acercaremos a las fórmulas matemáticas para calcular la longitud de una circunferencia.
L (longitud de la circunferencia) = D (diámetro) x "número pi" = 2 x "número pi" x r (radio).
Explicación de la fórmula para calcular la longitud de una circunferencia
Ejercicio sobre elementos de la circunferencia y rectas
Ejercicio sobre las partes de una circunferencia
Pasapalabra sobre geometría (Algunas preguntas no las hemos visto aún, pero las iremos viendo en lo que queda de curso. Puede ser un buen ejercicio de ampliación de conocimientos).
Explicación de la fórmula para calcular la longitud de una circunferencia
Ejercicio sobre elementos de la circunferencia y rectas
Ejercicio sobre las partes de una circunferencia
Pasapalabra sobre geometría (Algunas preguntas no las hemos visto aún, pero las iremos viendo en lo que queda de curso. Puede ser un buen ejercicio de ampliación de conocimientos).
Tema 11: Medir superficies.
Unidades de medida de superficie.
En primer lugar, en este tema descubrimos las unidades de superficie. Primero, hemos medido con 'cuadritos' para habituarnos y comprender qué es una superficie y su medida. Para, posteriormente, abordar las medidas estandarizadas de medida de superficies. Estas medidas ya nos son familiares, ya que son las mismas que las de longitud, pero con una diferencia: tienen un 2 pequeñito arriba. Lo que se llama "cuadrado". Concretamente metros cuadrados (m2), decímetros cuadrados (dm2) y milímetros cuadrados (mm2). Y hemos visto que existe una diferencia en la escalera que aprendimos en temas anteriores. Aquí, cada 'escaloncito' vale 100.
En primer lugar, en este tema descubrimos las unidades de superficie. Primero, hemos medido con 'cuadritos' para habituarnos y comprender qué es una superficie y su medida. Para, posteriormente, abordar las medidas estandarizadas de medida de superficies. Estas medidas ya nos son familiares, ya que son las mismas que las de longitud, pero con una diferencia: tienen un 2 pequeñito arriba. Lo que se llama "cuadrado". Concretamente metros cuadrados (m2), decímetros cuadrados (dm2) y milímetros cuadrados (mm2). Y hemos visto que existe una diferencia en la escalera que aprendimos en temas anteriores. Aquí, cada 'escaloncito' vale 100.Área de distintas figuras geométricas.
Finalmente, hemos aprendido fórmulas para hallar el área de diferentes polígonos y figuras geométricas. Yo les he comentado, que este tema es relativamente fácil ya que "solamente" tienen que aprenderse las 5-6 "fórmulas mágicas" y luego, en ellas, cambiar las letras por números y hacer las operaciones (cosa que aún no nos es tan sencilla porque seguimos sin sabernos las tablas de multiplicar al 100%).
Así pues, éstas son las "fórmulas mágicas" que tenemos que sabernos en este tema como el Padre Nuestro:
Rectángulo > A = b x a Cuadrado > A= l x l
Triángulo > A= (b x a) : 2 Romboide > A= b x a
Rombo > A= (D x d) : 2 Círculo > A= π x r2
Polígono regular > A= (p x a) : 2
Donde 'A' es área; 'b' es base; 'a' es altura, excepto en los polígonos regulares que es apotema; 'l' es lado; 'D' es diagonal mayor (la más grande); 'd' es diagonal menor (la más pequeña); 'p' es perímetro y 'r' es radio.
El resto de figuras "raras" que nos podamos encontrar y de las que debamos hallar su área. Simplemente tenemos que descomponerlas en algunas de estas figuras anteriores, calcular sus áreas individualmente y luego sumarlas.
Si nos sabemos esto perfectamente, tenemos el 50% del tema resuelto. "Solo" nos quedaría extraer los datos que nos dan, pensar qué tenemos que hacer y organizarnos y seguir los pasos que nos lleven a la solución. Lo que más nos cuesta vaya. Pero para eso practicamos día a día en la verbalización de los procesos. Es decir, que expliquemos con palabras y no solo con operaciones lo que tenemos que hacer para llegar a la solución.
Aquí os dejo algunos ejercicios para que practiquéis en casa:
Áreas de figuras geométricas 1
Áreas de figuras geométricas 2
Área de figuras geométricas 3
Áreas y perímetros 1
Áreas y perímetros 2
Áreas y perímetros 3
Áreas y perímetros 4
Así pues, éstas son las "fórmulas mágicas" que tenemos que sabernos en este tema como el Padre Nuestro:
Rectángulo > A = b x a Cuadrado > A= l x l
Triángulo > A= (b x a) : 2 Romboide > A= b x a
Rombo > A= (D x d) : 2 Círculo > A= π x r2
Polígono regular > A= (p x a) : 2
Donde 'A' es área; 'b' es base; 'a' es altura, excepto en los polígonos regulares que es apotema; 'l' es lado; 'D' es diagonal mayor (la más grande); 'd' es diagonal menor (la más pequeña); 'p' es perímetro y 'r' es radio.
El resto de figuras "raras" que nos podamos encontrar y de las que debamos hallar su área. Simplemente tenemos que descomponerlas en algunas de estas figuras anteriores, calcular sus áreas individualmente y luego sumarlas.
Si nos sabemos esto perfectamente, tenemos el 50% del tema resuelto. "Solo" nos quedaría extraer los datos que nos dan, pensar qué tenemos que hacer y organizarnos y seguir los pasos que nos lleven a la solución. Lo que más nos cuesta vaya. Pero para eso practicamos día a día en la verbalización de los procesos. Es decir, que expliquemos con palabras y no solo con operaciones lo que tenemos que hacer para llegar a la solución.
Aquí os dejo algunos ejercicios para que practiquéis en casa:
Áreas de figuras geométricas 1
Áreas de figuras geométricas 2
Área de figuras geométricas 3
Áreas y perímetros 1
Áreas y perímetros 2
Áreas y perímetros 3
Áreas y perímetros 4
Tema 12: Los cuerpos geométricos.
Después de haber trabajado las figuras planas en el tema anterior, en este último tema del curso nos centraremos en las figuras en 3D. Es decir, en los cuerpos geométricos. Aprenderemos cuáles son, sus características principales y cómo construirlos. En el siguiente esquema, resumo los conceptos principales del tema. También pueden ver los vídeos.
Practica aquí >
Prismas y pirámides
Cuerpos redondos
* En estos ejercicios puede haber cosas que no hayamos trabajado o que llamen de otra forma. Por ejemplo: en los ejercicios distinguen "aristas básicas" (las de la base) de aristas laterales. Nosotros no lo hacemos, y hablamos simplemente de aristas).
Practica aquí >
Cuerpos redondos
* En estos ejercicios puede haber cosas que no hayamos trabajado o que llamen de otra forma. Por ejemplo: en los ejercicios distinguen "aristas básicas" (las de la base) de aristas laterales. Nosotros no lo hacemos, y hablamos simplemente de aristas).
Repaso final de curso
Una vez terminado el temario de este curso, nos vamos a centrar en aquello aspectos más importantes y que tenemos que tener bien fijados de cara ya al próximo curso. Estos contenidos sobre los que vamos a volver a trabajar son: operaciones con fracciones, operaciones con decimales y cálculo de áreas. Vayamos por partes:
Operar con fracciones
En el último tema del primer trimestre (tema 4) aprendimos a hacer operaciones básicas con fracciones (sumas y restas), además de los números mixtos y los porcentajes. Así pues, vamos a recordar primero un poco la teoría, los pasos a seguir.
Sumar y restar fracciones
Como ya sabemos, para sumar y restar con fracciones seguimos los mismos pasos, lo hacemos todo exactamente igual, solo que al final, en el último paso, en una sumamos y en otra restamos, obviamente. Aquí los pasos a seguir en las dos posibilidades que nos podemos encontrar:
Con igual denominador
1º) Dejamos el mismo denominador.
2º) Sumamos o restamos numeradores.
Con distinto denominador
1º) Buscamos común denominador para todas las fracciones. Para ello:
a) Buscamos el primer múltiplo común de los denominadores. Una vez ya tenemos el denominador común, dividimos este nuevo denominador común entre los antiguos y multiplicamos por los numeradores. Así obtenemos los nuevos numeradores de nuestras fracciones.
b) Multiplicamos los denominadores entre sí y obtenemos el nuevo denominador común. Después multiplicamos en cruz (el numerador de una por el denominador de otra) para obtener los numeradores.
2º) Mantenemos el mismo nuevo denominador común.
3º) Sumamos o restamos los nuevos numeradores.
Practica aquí > Sumas y restas con fracciones
Sumas y restas con fracciones 2
Sumas y rectas con fracciones 3
Sumas y restas con fracciones 4
Sumas y restas con fracciones 5
Como ya sabemos, para sumar y restar con fracciones seguimos los mismos pasos, lo hacemos todo exactamente igual, solo que al final, en el último paso, en una sumamos y en otra restamos, obviamente. Aquí los pasos a seguir en las dos posibilidades que nos podemos encontrar:
Con distinto denominador
Practica aquí > Sumas y restas con fracciones
Sumas y restas con fracciones 2
Sumas y rectas con fracciones 3
Sumas y restas con fracciones 4
Sumas y restas con fracciones 5
Multiplicar fracciones o un número por una fracción
Para multiplicar fracciones es muy sencillo: multiplicamos los numeradores entre sí y los denominadores entre sí. Es decir, numerador por numerados y obtenemos el resultado del numerador; y denominador por denominador y obtenemos el resultado del denominador.
Por otra parte, para multiplicar un número por una fracción, lo hacemos de la misma forma. Simplemente, tenemos que recordar que un número siempre lleva denominador 1, lo que pasa es que no lo ponemos. Recordando esto, después lo multiplicamos como si fueran dos fracciones.
Para multiplicar fracciones es muy sencillo: multiplicamos los numeradores entre sí y los denominadores entre sí. Es decir, numerador por numerados y obtenemos el resultado del numerador; y denominador por denominador y obtenemos el resultado del denominador.
Por otra parte, para multiplicar un número por una fracción, lo hacemos de la misma forma. Simplemente, tenemos que recordar que un número siempre lleva denominador 1, lo que pasa es que no lo ponemos. Recordando esto, después lo multiplicamos como si fueran dos fracciones.
Dividir fracciones
Esto no lo hemos visto durante el curso, pero sí que lo hemos mencionado en este repaso de final de curso; ya que es sencillo y nos viene bien de cara al próximo curso. Para dividir fracciones, simplemente multiplicamos los números en cruz. Es decir, el numerador de la primera por el denominador de la segunda (y obtenemos el resultado del numerador); y el denominador de la primera por el numerador de la segunda (y obtenemos el resultado del denominador). Así de sencillo. Lo que no debemos olvidar, aunque parezca contradictorio, es que para dividir fracciones, multiplicamos en cruz, no dividimos en cruz.
Practica aquí > Operaciones con fracciones
Operaciones con números decimales
Para operar con decimales debemos tener algunas cosas en cuenta en cada operación:
Sumar y restar decimales
Lo más importante para estas dos operaciones es que coloquemos bien los números. Es decir, que las comas estén una debajo de la otra y luego, las decenas debajo de las decenas, las unidades debajo de las unidades, las décimas debajo de las décimas,... Y luego sumamos y restamos normal, sin olvidarnos de poner la coma.
Lo más importante para estas dos operaciones es que coloquemos bien los números. Es decir, que las comas estén una debajo de la otra y luego, las decenas debajo de las decenas, las unidades debajo de las unidades, las décimas debajo de las décimas,... Y luego sumamos y restamos normal, sin olvidarnos de poner la coma.
Multiplicar números decimales
Para multiplicar números decimales, lo hacemos olvidando (en un principio) que son números decimales. Es decir, los colocamos sin tener en cuenta las comas, como si fuera una multiplicación de números enteros. De derecha a izquierda sin más. Y una vez que hemos hecho la multiplicación normal, contamos cuantas cifras decimales tiene que cada uno de los números que hemos multiplicado, las sumamos y se las colocamos en el resultado; comenzando por la derecha. Por ejemplo, si multiplicamos dos números con dos cifras decimales cada uno, nuestro resultado va a tener cuatro cifras decimales.
Dividir con números decimales
Aquí tenemos dos posibilidades:
1) Que el número decimal sea el dividendo: entonces hacemos la división normal, simplemente teniendo en cuenta que cuando nos toque bajar la cifra que va después de la coma, antes tenemos que ponerle la coma al cociente. Y seguimos dividiendo normalmente.
2) Que el divisor sea un número decimal: aquí sí nos molesta la coma. Para ello multiplicamos el divisor por la unidad seguida de tantos ceros (10, 100, 1000,...) como cifras decimales tenga el divisor. Posteriormente, multiplicamos el dividendo por el mismo número (10, 100, 1000...). Una vez que la coma ya ha desaparecido del divisor (no tiene por qué haber desaparecido del dividendo) hacemos ya la división normal.
Aquí tenemos dos posibilidades:
1) Que el número decimal sea el dividendo: entonces hacemos la división normal, simplemente teniendo en cuenta que cuando nos toque bajar la cifra que va después de la coma, antes tenemos que ponerle la coma al cociente. Y seguimos dividiendo normalmente.
2) Que el divisor sea un número decimal: aquí sí nos molesta la coma. Para ello multiplicamos el divisor por la unidad seguida de tantos ceros (10, 100, 1000,...) como cifras decimales tenga el divisor. Posteriormente, multiplicamos el dividendo por el mismo número (10, 100, 1000...). Una vez que la coma ya ha desaparecido del divisor (no tiene por qué haber desaparecido del dividendo) hacemos ya la división normal.
Cálculo de áreas
Finalmente, en los últimos días ya del curso, hemos vuelto a repasar cómo calcular el área de una superficie. Estos conceptos los deberíamos de tener "frescos", ya que ha sido el penúltimo tema que hemos trabajado en el curso. Para volverlo a trabajar, lo hemos hecho de forma algo más práctica, por parejas y tomando nuestras propias medidas sobre el terreno. De esta forma, hemos calculado el área del arenero, de la zona infantil y de los arcos de la zona techada del patio.
*Para practicar con el cálculo de superficies, subir y mirar lo escrito en el tema 11.
Finalmente, en los últimos días ya del curso, hemos vuelto a repasar cómo calcular el área de una superficie. Estos conceptos los deberíamos de tener "frescos", ya que ha sido el penúltimo tema que hemos trabajado en el curso. Para volverlo a trabajar, lo hemos hecho de forma algo más práctica, por parejas y tomando nuestras propias medidas sobre el terreno. De esta forma, hemos calculado el área del arenero, de la zona infantil y de los arcos de la zona techada del patio.
*Para practicar con el cálculo de superficies, subir y mirar lo escrito en el tema 11.
Este comentario ha sido eliminado por el autor.
ResponderEliminarComo compañero tuyo y coordinador TIC del centro me encanta que uses las nuevas tecnologías para facilitar el aprendizaje de nuestros alumnos. Un abrazo.
ResponderEliminarRichard puedes poner algo del minimo comun multiplo y de maximo comun divisor es que no me ubico muy bien. Gracias😁
ResponderEliminarMe gusta mucho tu blog.
ResponderEliminarComo te llamas en youtube richard😜
ResponderEliminar